Shoving Ace-High Preflop (With Math!)

I started a thread in the forum about a hand I played at a poker club in Portland. The thread started a lot of discussion with differing views, and I wanted to expand a bit on what I did and why I did it. This is the kind of exploration you should be doing on your own as well, and if you’ve never done this kind of math before, this post may seem a bit advanced. But fear not, we’ll get through this together and be better for it!

With that said, here is the hand:

• Hero (SB): $250. I’ve been very tight for the last hour since the table has been pretty loose, and I’ve been getting zero hands/spots.
• BB: $100. Just reloaded for his third $100 after spewing off $100 preflop the last two hands in a row. He’s visibly tilting.
• UTG: $300. Thinking player who needs people to know he’s a smart guy.
• MP1: $800. Running like God, allegedly doesn’t like to gamble and took longer than he should have to stack off AQ preflop against the BB in the previous hand. Doesn’t seem tricky.

UTG limps, MP1 limps, folds to me in the SB with A♠ 7♠

I complete and the tilty BB quickly makes it $20.

In the actual hand the action folded back to me, and when I posed that action, many posters said they would fold. Since I’m a huge nerd and I love explorative work, let’s analyze this hand and see which action would be best. When it folds to me I have 3 options: fold, call, or re-raise.

In this spot calling would be terrible. It would leave us out of position in a less-than-2 small SPR pot with a terrible hand. So we can automatically get rid of that option. And any re-raise is essentially a shove. Even if we re-raised to $50, if he shoves we are getting 3:1 and almost surely have enough equity to call. Given that, our options are really just between folding and shoving. And if shoving is +EV, then we shove…if shoving is –EV, we fold. Easy enough.

You may be wondering how we solve for shoving here. To do that we just need some important poker tools like Equilab, a fold equity calculator, and if you really like nerding out, a spreadsheet to do the work in. Let’s start by building an EV equation so we can create a framework, then we’ll run the EV with various assumptions and see how a shove here would perform. If you’ve never set up an EV equation, I suggest first watching this video which shows the process:

If we shove there are three possible outcomes:

1. We shove and he folds
2. We shove, he calls, and we win
3. We shove, he calls, and we lose

That’s easy enough, right? When we shove (and again, any 4bet is an effective shove given the stack depth) and he folds, we pick up $26 dollars uncontested (his $20 raise + 2 limps + our completion, which no longer belongs to us in this equation). When we shove and win, we win his $100 + 2 limps + our completion for a total of $106. And when we shove and lose, we lose $98 since that’s the total risk of our shove (remembering again that our $2 completion doesn’t belong to us anymore).

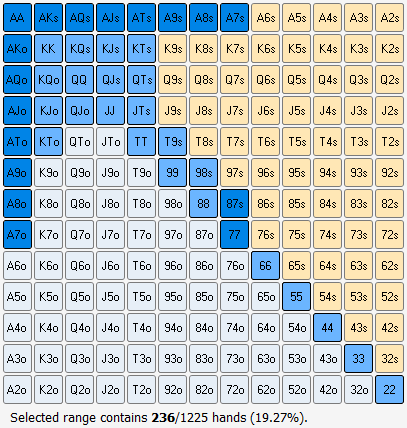
Now we can just plug in some percentages and go to work. First, what kind of equity would we have if we jammed and he called? Let’s first assume he would call with a range of 99+/AQ+, a reasonable range for him to raise to $20 and call with. If we plug that into Equilab we have 30% equity.

The last number we need to estimate is how often he would fold after we 4bet. Let’s assume he would never fold, which inherently means the range he would raise to $20 with is exclusively 99+/AQ+ (I don’t think this is true, but bear with me for a moment). So when we plug all of the numbers in we see this:

With those assumptions this would be a terrible jam, losing us about $37 each time we make it. But let’s say the range he would raise to $20 with is much wider than just 99+/AQ+, and thus we can expect some percentage of folds from him. Let’s assume that 99+/AQ+ only makes up 25% of his raising range, which means we could expect folds from him 75% of the time. If that’s the case we notice our EV jumps up considerably:

This should be obvious though. The more often we are able to pick up the $26 uncontested, the better and better our shove will be. But things can also get better when our equity increases when he calls our jam. For instance, say he would raise to $20 and call our jam with 77+/AT+/KQ. Now our equity jumps up to 35%. If we assume he raise/folds 60% of the time then our shove nets us about $5.

In a nutshell, if our equity goes up, our EV goes up. If he folds more preflop, our EV goes up. If he folds more AND our equity increases, then our EV goes WAY up. For instance, in this situation I actually thought he’d tilt call with a much wider range of hands. In a normal situation I would never assume a player to call this wide, but I realistically thought he’d call with all pairs, many Broadway combos and some suited connectors. No, a good player would never do this. But a bad player who’s on tilt? And one who seems to be on a mission to see how much money he can burn in an orbit seems like a prime candidate to shove a range where I have 44% of equity. And if he raise/folds 50% of the time I’m making a +$9 shove here:

The other big thing to consider is how often is he raising to $20 preflop? The previous range I assigned, the one that gave me a whopping 44% equity, was actually 19% of hands preflop (hand-created, not just dragging the bar to 19% of hands).

What we can do is plug the numbers into a fold equity calculator to figure out how wide he actually needs to be opening at a minimum. So let’s plug everything in real quick:

We notice that we need him to fold 24% of the time for this to be a breakeven shove, given the parameters we’ve set. If he folds much more than 24% of the time, then this is +EV, and if he folds less than 24% of the time, this will be a losing shove. But what does this 24% number actually mean? I’m so glad you asked!

I assumed he’d raise/call with 19% of hands. But we need some folds for this to be profitable. So we can take 19% and divide it by 76% (100% minus the 24% given above), then multiply it by 100 to find the breakeven number of hands he needs to be raising to $20 with:

(19%/76%) * 100 = 25%

This means if we think he’s raising to $20 with exactly 25% of hands, and calling with 19% of total hands, this jam is breakeven. But because he’s tilting, isn’t it reasonable to assume that he’s likely raising to $20 with a MUCH wider range and thus he’s able to raise/fold more often? Or, if he raises to $20 really wide and actually calls the jam wider (because he’s tilting of course), then our equity goes up and the shove becomes even better. It’s a win/win!

Now, there are a few caveats here. First, this is all work we do away from the table. Exploring breakeven points, figuring out our EV, understanding our equity, etc. Second, the more of this work you do away from the table, the easier it is to eyeball it correctly in real-time. Third, this is a special situation because I assumed his opening range was way wide. This either meant I could expect a lot of folds from him OR I could expect a massive equity jump with fewer folds. Either way I expected this to be +EV. However, with different assumptions this shove could go from +EV to super –EV in a heartbeat. It was my off-table explorations that allowed me to correctly estimate this spot in real-time.

In the end he ended up snap-calling me with QJo, and I somehow held. But the result isn’t nearly as important as understanding the work that goes into choosing a +EV line at the table. Now go explore one of your own hands and see if you could have made a cool shove and uncovered some fun EV!

WHAT CAN ONE RED CHIP GET YOU?

A single red chip is all it takes to enroll in CORE today. This is the most complete poker course ever created, taking you from the poker fundamentals you NEED to know all the way to the advanced plays you WANT to know. Enroll and jump into your first lesson now ♥

ENROLL FOR JUST $5